Thread Dial Indicator - Inch and Metric

email: t ony@lathes.co.uk
Home Machine Tool Archive Machine-tools Sal e & Wanted
Machine Tool Manuals Catalogues Belts Books Accessories

Universal Thread Dial Indicator - Inch and Metric
Continued on Page 2 Engineering Drawings Page 3

A very clever design for a universal thread-dial indicator (DTI) that can be used for both metric and inch screwcutting. The designer and builder, Daniele Marzocchi, is an Italian, living in Germany, hence the text in German, with further details can be found here. https://forum.zerspanungsbude.net/viewtopic.php?f=10&t=62888.
A beautifully made artefact, the unit is shown fitted to the designer's own lathe that has a 3 mm pitch leadscrew. The designer writes:
I managed to find a method to calculate the gearing for thread dial indicator that can be used on a metric lathe when generating both inch and metric pitches. Using this method, anyone is potentially able to construct their own custom-made thread dial indicator with all the necessary gears
There are three mathematical quantities that determine the construction of a thread dial indicator:
1) Ratio between thread pitch being generated and the pitch of the leadscrew
2) Number of teeth on the gear that meshes with the lead screw - the number of teeth on this gear should always be a multiple of the pitch of the lead screw. For example: leadscrew pitch is 6 mm, the number of teeth on the DTI will be 12 or 24 or 48
3) The number of lines on the rotary dial plate. This is always related to the number of teeth on the DTI's gear, as well as the number of times the half nut can be closed..

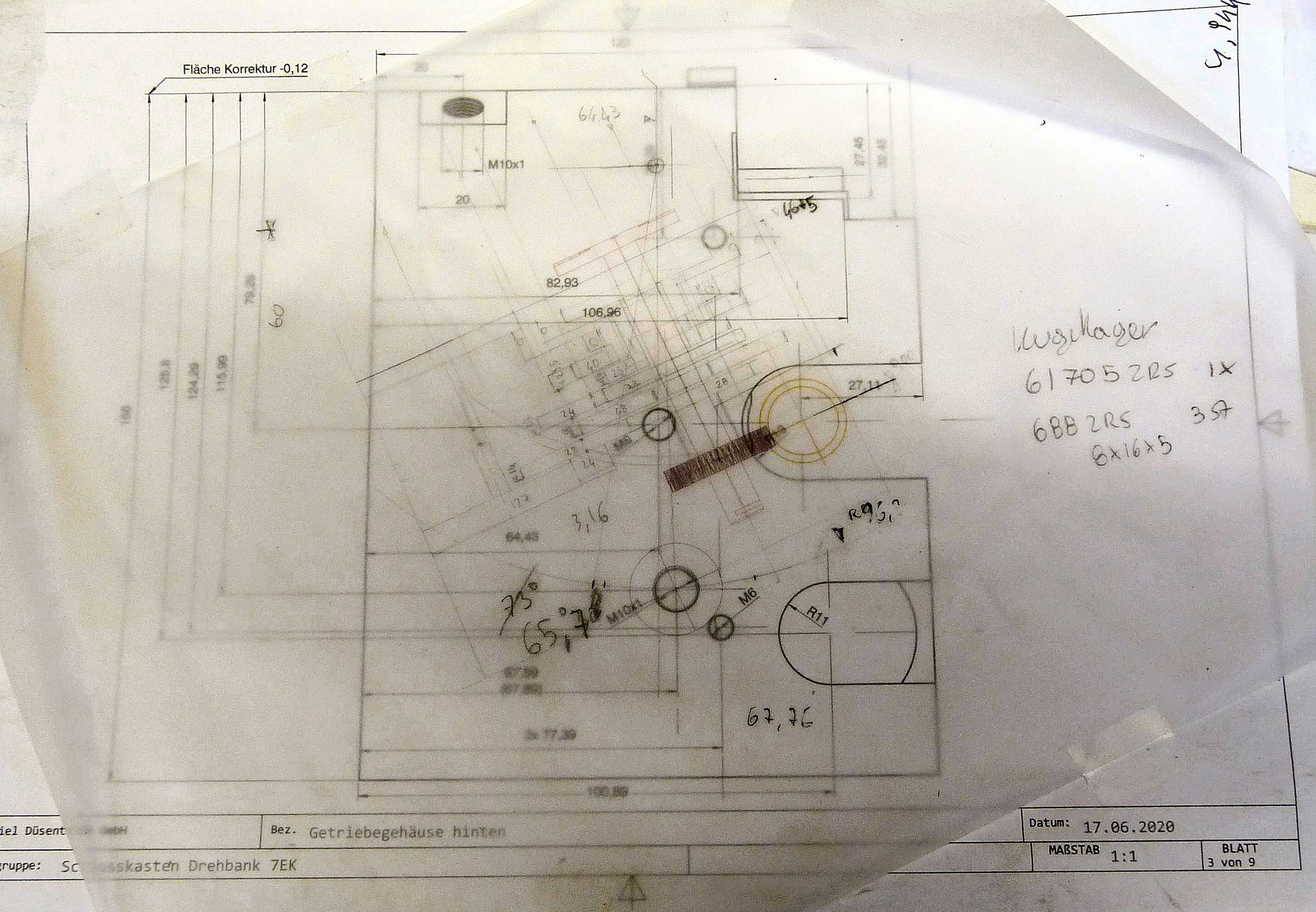
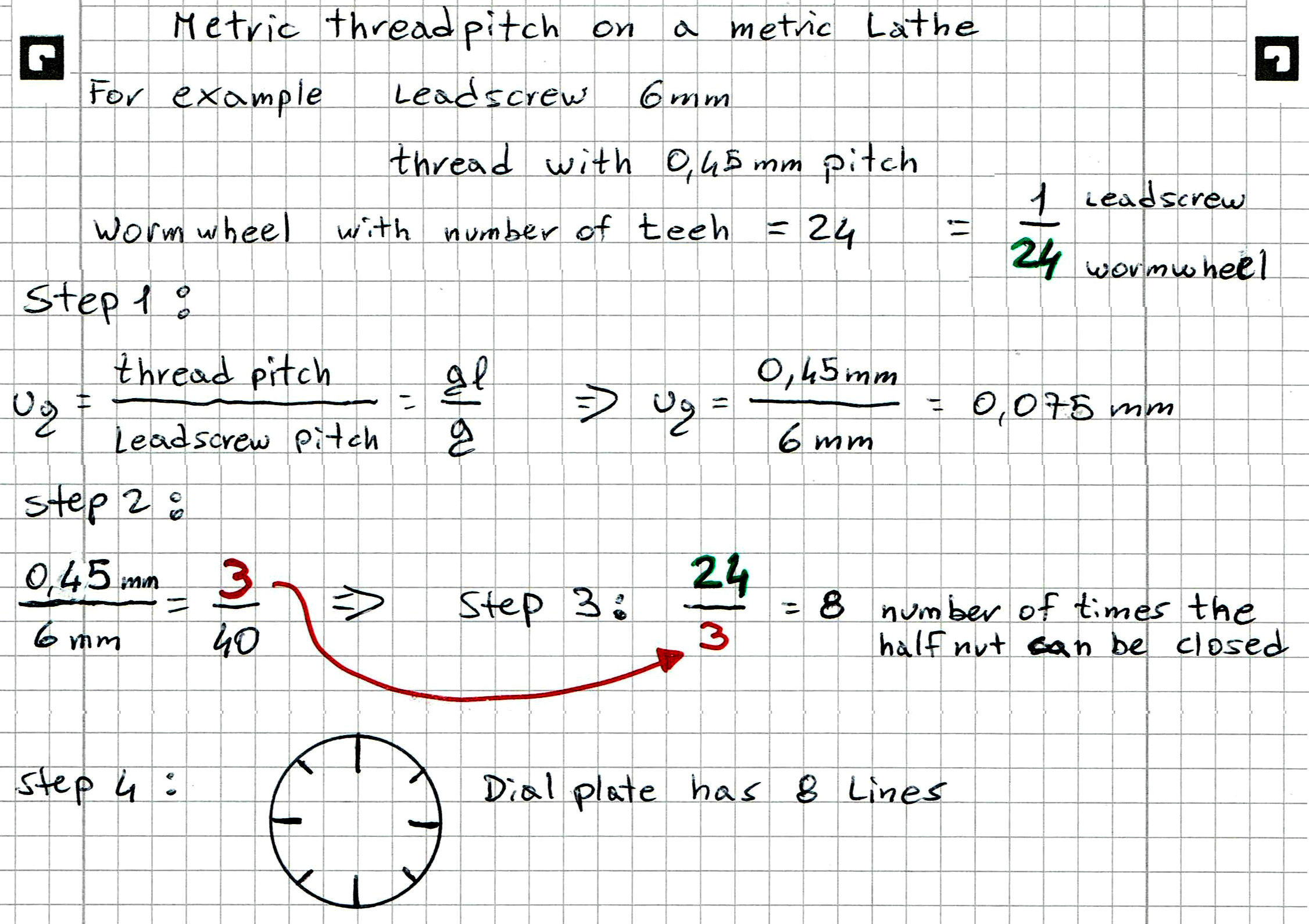
1° step: Calculate the ratio between the thread pitch and the leadscrew pitch.
2° step: the mathematical fraction obtained is rounded down to the lowest whole numbers
3° step: Division of the now obtained counter into the number of teeth of the worm wheel (pinion)
4° step: The result obtained in this way indicates how many times the half nut can be closed for each revolution of the dial
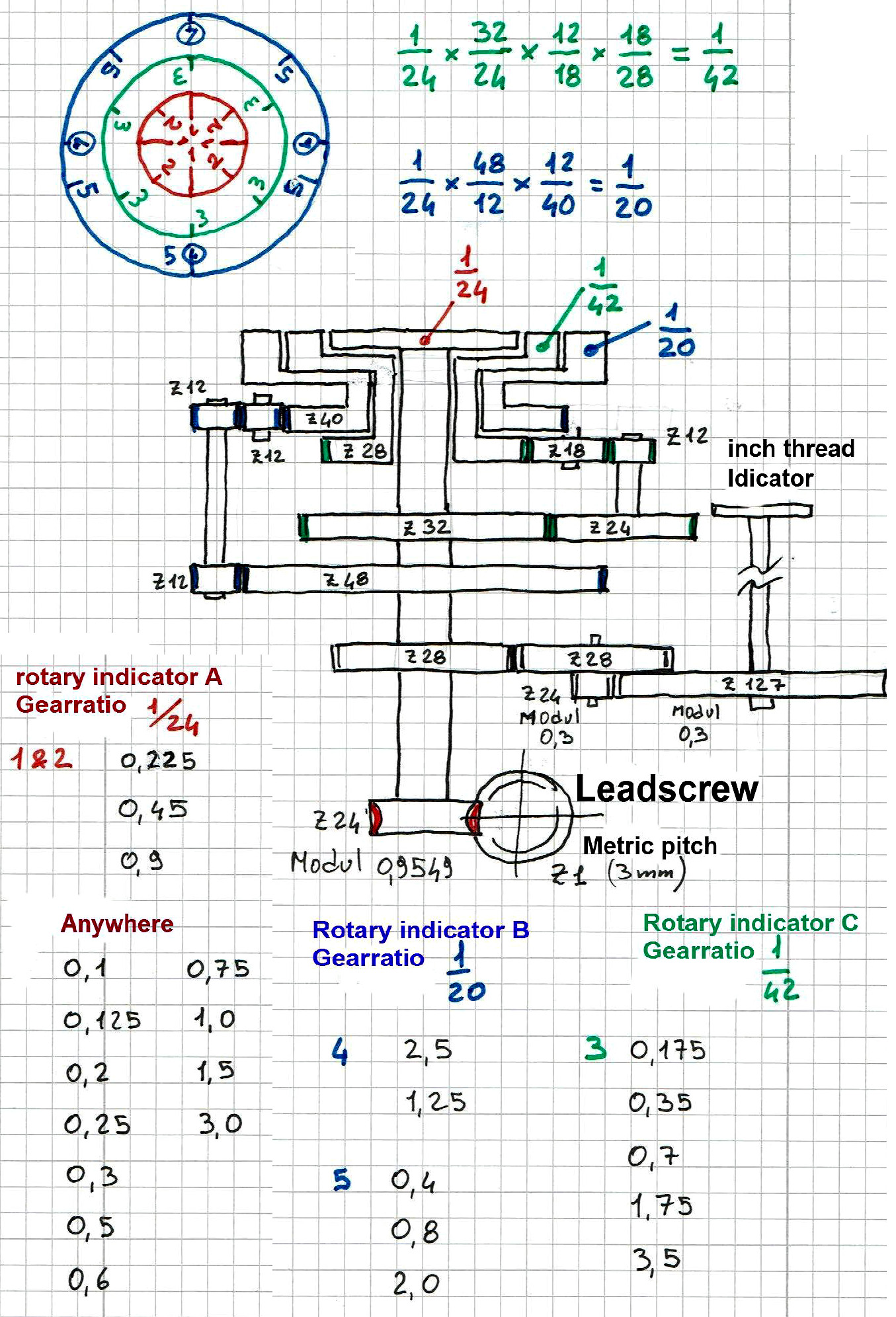
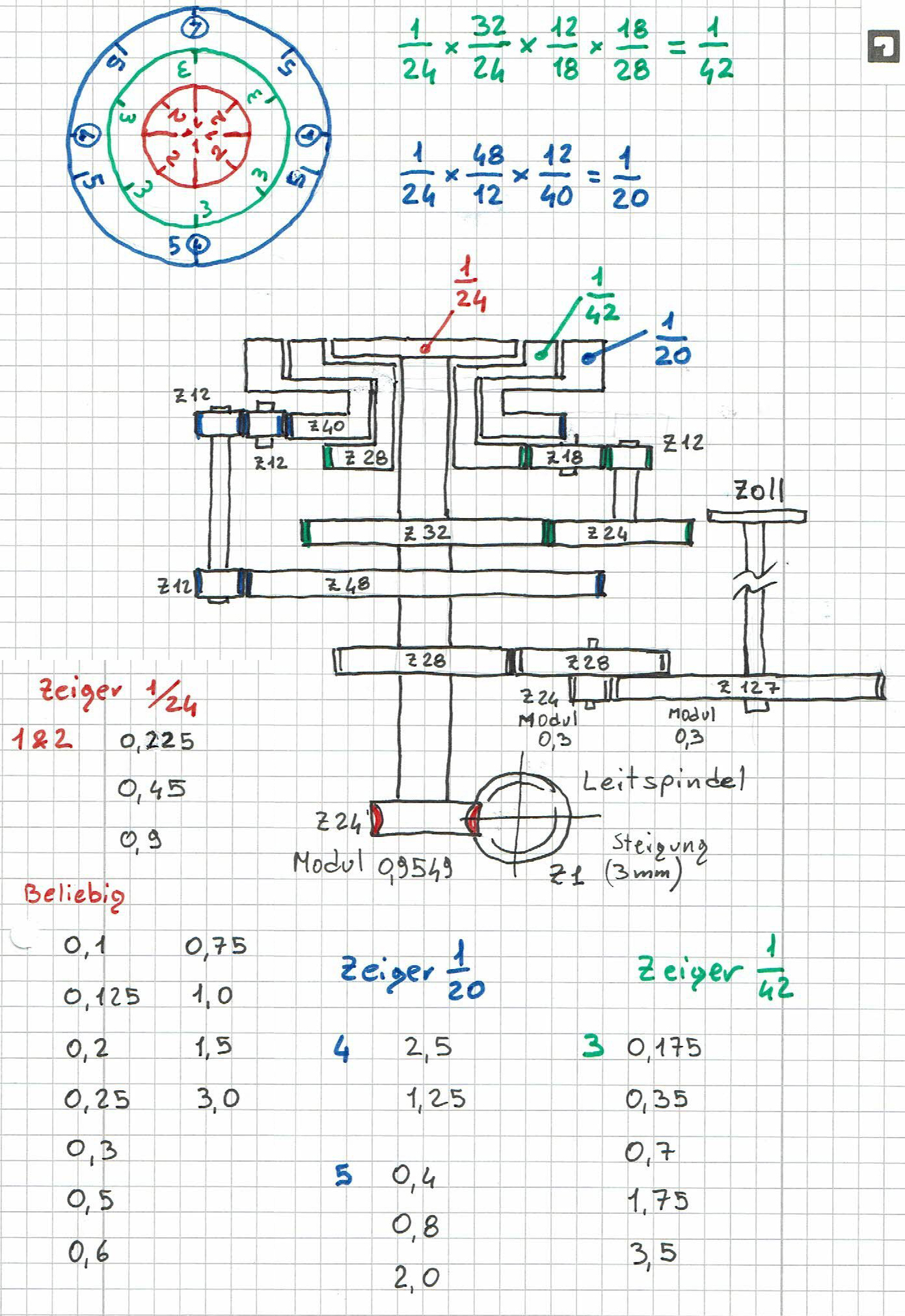
My design takes into account all threads with a dividend number of 2, 3, 4, 5, 7 and 127 for inch pitches (127 revolution of the leadscrew before the next time the halfnut can be closed. But not 11 and therefore thread pitches of 5.5 and 11 mm not detectable).
For metric threads, the total list of pitches can be divided into groups with each group determining which dividend number the affected thread pitch remains as a multiple of. For example:
dividend number is 5, metric tread M8 has 1,25 mm then 5 divided by 1. 25 = 4 (whole number).
dividend number is 7, thread 0,35 then 7 divided by 0.35 = 20 (whole number)
A very good explanation of this can be found here
https://www.youtube.com/watch?v=zG9XYDCDwWY&ab_channel=AnEngineer%27sFindings - this was my inspiration to develop the thread clock construction.
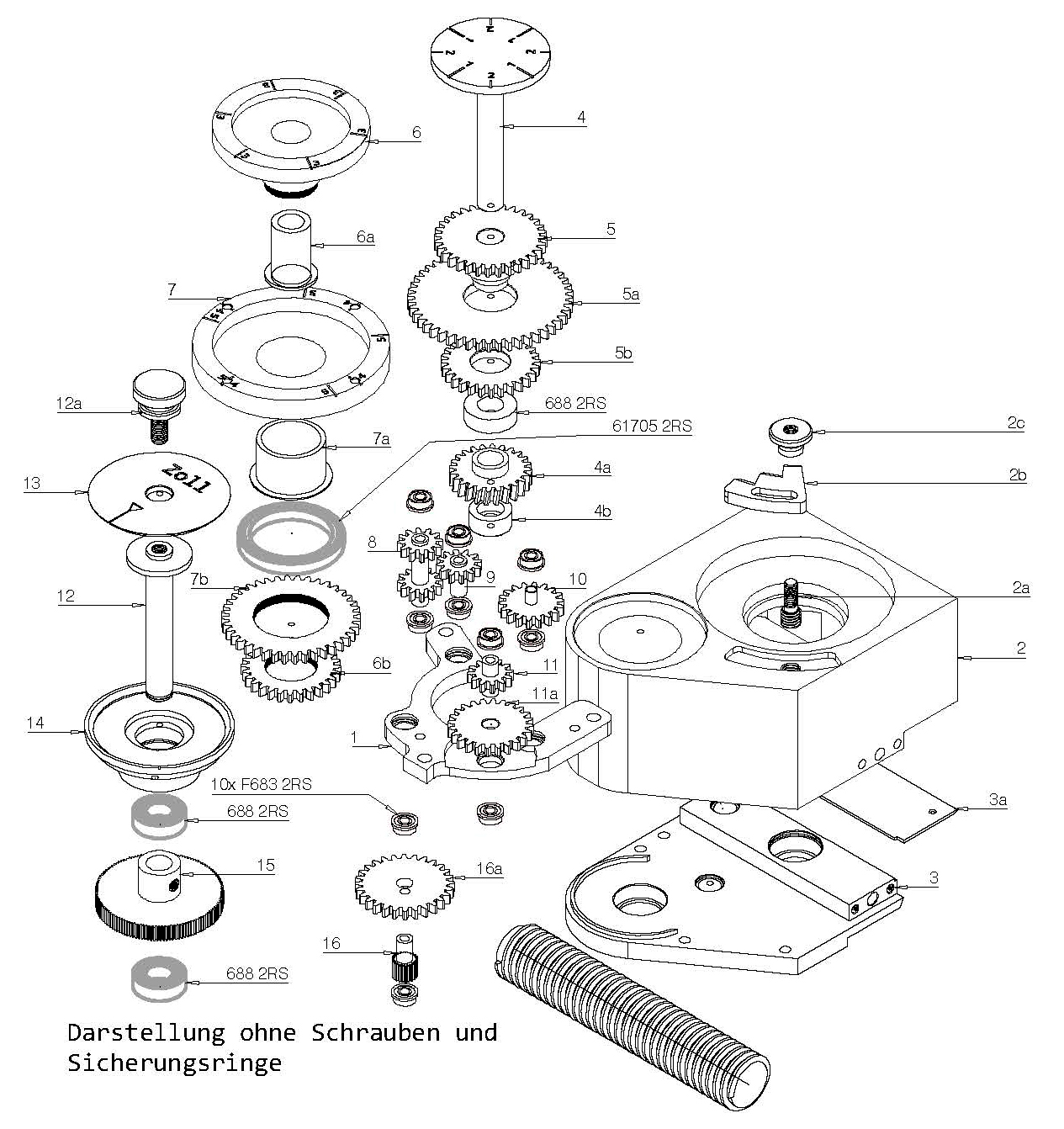
And so, with the principle that every mathematical fraction as well as gear ratio can be expanded as desired, I have the original ratio of 1/24 (lead screw/worm wheel) to 3 additional gear ratios which also has other thread pitches with 3 additional rotary dial plates covering all dividend numbers groups (2, 3, 4, 5, 7 and 127).
Extra information for leadscrew with other pitches can be found here:
https://forum.zerspanungsbude.net/viewtopic.php?f=10&t=62888&start=10
Translation: Striche = Lines (on the dialplate)..